[最も欲しかった] trig identities tan^2 136393-Trig identities tan^2

Trigonometry Identities Examples and Strategies cosine is an even identity;Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyI'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\sec

Derivatives Of Trigonometric Functions

Trig identities tan^2

Trig identities tan^2-Cos^2 x sin^2 x = 1 sin x/cos x = tan x You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more some other identities (you will learn later) include cos x/sin x = cot x 1 tan^2 x = sec^2 x 1 cot^2 x = csc^2 x hope this helped!Trig identities Trigonometric identities are equations that are used to describe the many relationships that exist between the trigonometric functions Among other uses, they can be helpful for simplifying trigonometric expressions and equations The following shows some of the identities you may encounter in your study of trigonometry

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

Derivatives of Trigonometric Functions The basic trigonometric functions include the following 6 functions sine (sinx), cosine (cosx), tangent (tanx), cotangent (cotx), secant (secx) and cosecant (cscx) All these functions are continuous and differentiable in their domainsStudents are taught about trig identities or trigonometric identities in school and are an important part of higherlevel mathematics So to help you understand and learn all trig identities we have explained here all the concepts of trigonometryAs a student, you would find the trig identity sheet we have provided here useful So you can download and print the identities PDFSimplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 1

Let's quickly recap the major steps and ideas that we discovered in our previous lesson Can we plug in values for the angles to show that the leftHere we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead oneTrig Identities Cheat Sheet admin July 10, 18 When solving, simplify with the identities initially, if you can Trigonometric identities are used to manipulate the trigonometric equations of some specific forms In this video, the Pythagorean identities and the way they are derived are shown In mathematics, there are numerous logarithmic

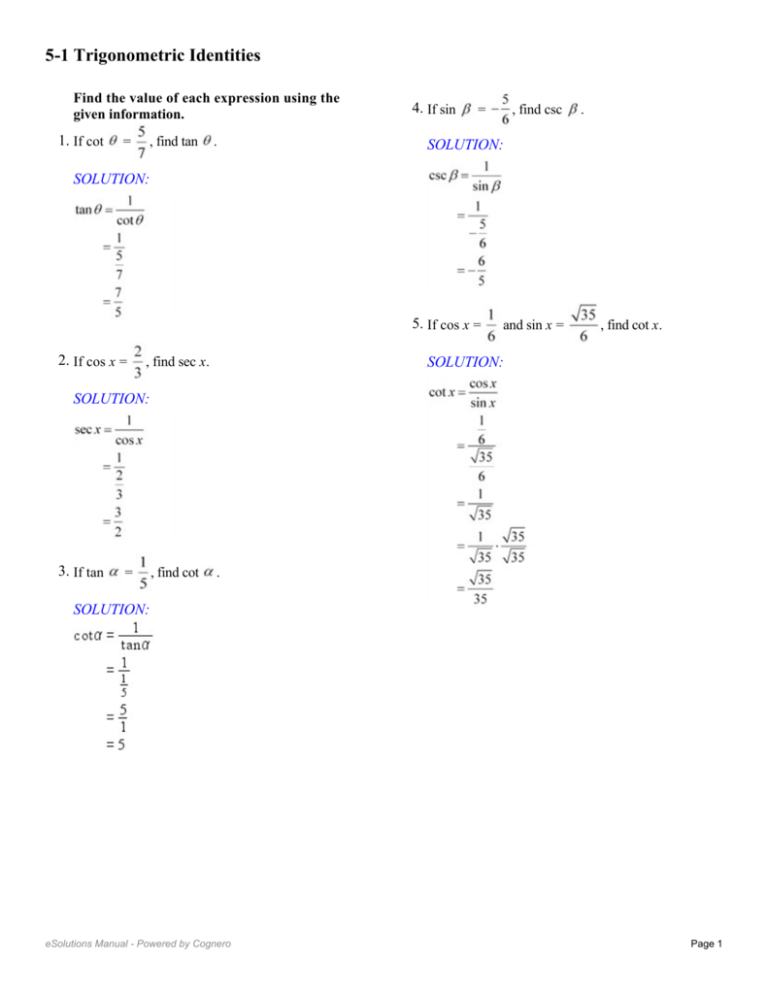
Example 2 Verify that tan (180°Trig Equations and Identities wwwnaikermathscom 4 (a) Given that sin q = 5 cos q, find the value of tan q (1) (b) Hence, or otherwise, find the values of q in the interval 0 £This is a matter of experience, familiarity and recognition Practice as many questions as possible Be familiar with trigonometric functions that can be integrated easily Be familiar with common identities – especially squared terms sin2 x, cos2 x, tan2 x, cosec2 x, sec2 x, tan2 x all appear in identities

Solved We Wish To Prove The Following Trig Identity Cos Chegg Com

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

Tan is an odd identity quotient identity (for tangent) algebra/ simplify 1) 2) cos tan (x) Strategy 1) get rid of the negatives 2) üy to change terms to sin's and COS's 3) simplFy • tan (x) tan x sm x cos x smx cos (x) cosx • cosx • Prove Strategy62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identitiesTrig Cheat Sheet Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p <<q or 0°<q<°90 opposite sin hypotenuse q= hypotenuse csc opposite q= adjacent cos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any

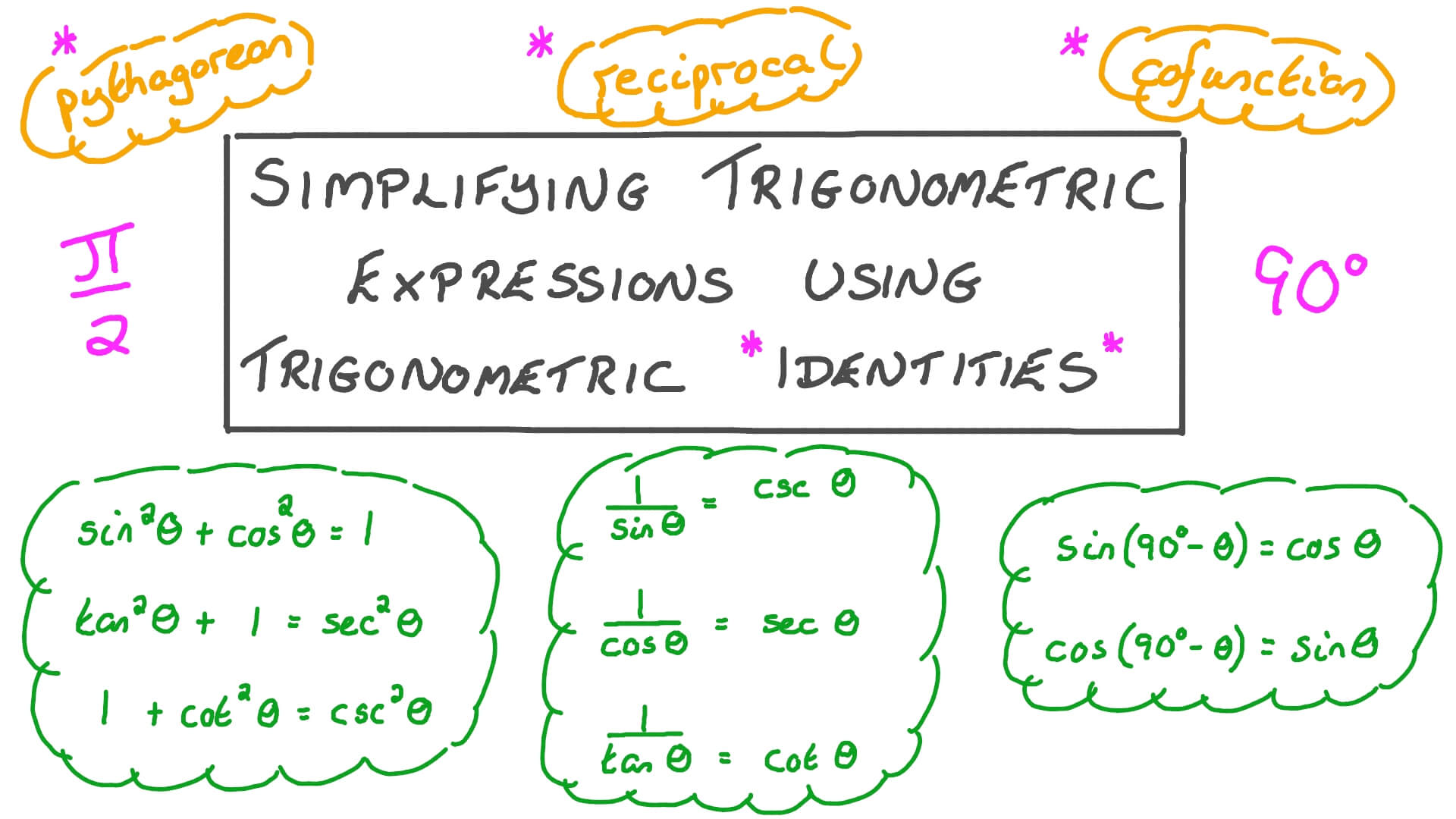
Lesson Video Simplifying Trigonometric Expressions Using Trigonometric Identities Nagwa

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Now that we have become comfortable with the steps for verifying trigonometric identities it's time to start Proving Trig Identities!Trigonometric Identities 43 Introduction A trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles) There are a very large number of such identities In this Section we discuss only the most important and widely used Any engineer using trigonometry in an applicationTRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u

6 1 2 Trigonometric Identities

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Trigonometric Identities Solver \square!Difference Identities sin( )=sin cos cos sinThe trigonometric ratios are defined for right angled triangles The relationships between trigonometric ratios per Pythagorean theorem are called Pythagorean Trigonometric Identities sin2θ cos2θ = 1 sin 2 θ cos 2 θ = 1 It is noted that the result is true for any value of θ θ That is, if θ = 27 θ = 27, then sin227∘ cos227

List Of Trigonometric Identities Wikipedia

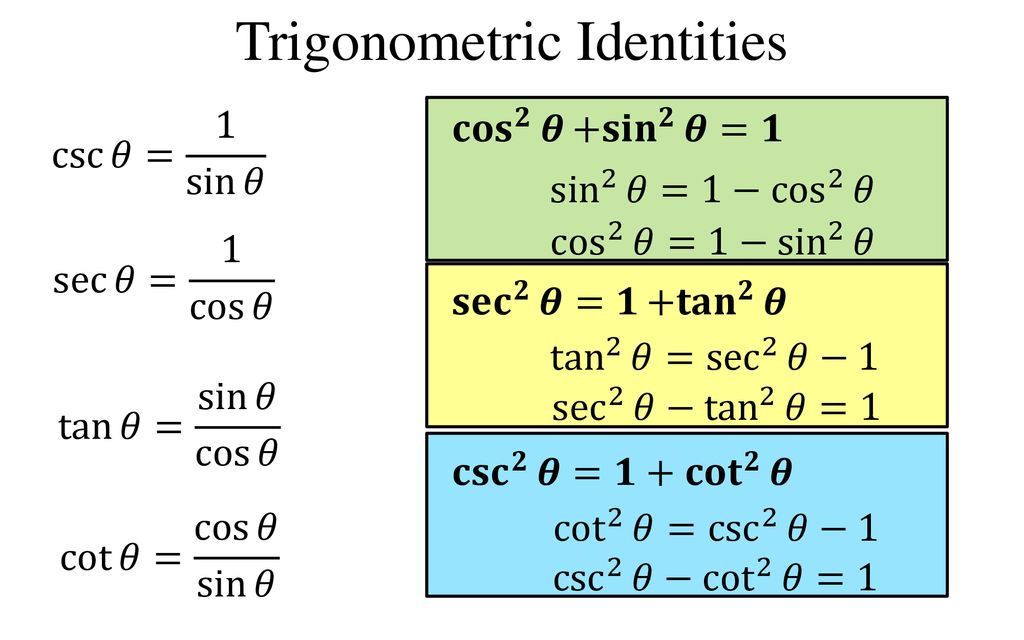
Trigonometric Identities And Equations Ppt Download

X) = tan x Example 4 Verify that tan (360°The key Pythagorean Trigonometric identity are sin2(t) cos2(t) = 1 tan2(t) 1 = sec2(t) 1 cot2(t) = csc2(t)Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Summary Of Trigonometric Identities

Important Trigonometric Identiti

− x) = −tan x Example 3 Verify that tan (180°Trigonometric Identities Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identitiesSection 12 Integrals Involving Trig Functions 5 Evaluate ∫ sec6(3y)tan2(3y) dy ∫ sec 6 ( 3 y) tan 2 ( 3 y) d y Hint Pay attention to the exponents and recall that for most of these kinds of problems you'll need to use trig identities to put the integral into a form that allows you to do the integral (usually with a Calc I

Verifying Trigonometric Identities Process Make One Side Look

Trigonometric Identities

− x) = − tan x The preceding three examples verify three formulas known as the reductionIn this first section, we will work with the fundamental identities the Pythagorean Identities, the evenodd identities, the reciprocal identities, and the quotient identities We will begin with the Pythagorean Identities (see Table 1 ), which are equations involving trigonometric functions based on the properties of a right triangleRecall the definitions of the trigonometric functions The following indefinite integrals involve all of these wellknown trigonometric functions Some of the following trigonometry identities may be needed A) B) E) It is assumed that you are familiar with the following rules of differentiation

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Tangent Identities

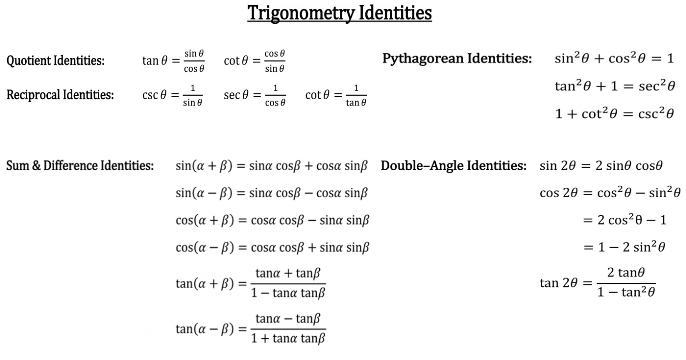
Some Useful Trigonometric Identities An identity is an equation whose left and right sides when defined are always equal regardless of the values of the variables the two sides contain Some very useful trigonometric identities are shown belowTo determine the difference identity for tangent, use the fact that tan(−β) = −tanβ Example 1 Find the exact value of tan 75°Trigonometry Identities Quotient Identities tan𝜃=sin𝜃 cos𝜃 cot𝜃=cos𝜃 sin𝜃 Reciprocal Identities csc𝜃= 1 sin𝜃 sec𝜃= 1 cos𝜃 cot𝜃= 1 tan𝜃 Pythagorean Identities sin2𝜃cos2𝜃=1 tan 2𝜃1=sec2𝜃 1cot2𝜃=csc2𝜃 Sum &

1

Chapter 5 Trigonometric Identities Review Sheet

SubsectionUsing Trigonometric Ratios in Identities 🔗 Because the identity 2x2 − x − 1 = (2x 1)(x − 1) 🔗 is true for any value of x, it is true when x is replaced, for instance, by cosθ This gives us a new identity 2cos2θ − cosθ − 1 = (2cosθ 1)(cosθ − 1) 🔗Here are sixteen Trigonometric Identities SIN = Sine COS = Cosine TAN = Tangent CSC = CoSecant SEC = Secant COT = CoTangent #1 1 SIN Θ = CSC Θ #2 1 COS Θ = SEC Θ #3 SIN Θ TAN Θ = COS Θ #4 COS Θ 1 COT Θ = = SIN Θ TAN Θ #5 1 SEC Θ = COS Θ #6 1 CSC Θ = SIN Θ #7 SIN 2 Θ COS 2 Θ = 1 #8 SEC 2 Θ = 1 TAN 2Sin 2 (x) cos 2 (x) = 1 tan 2 (x) 1 = sec 2 (x) cot 2 (x) 1 = csc 2 (x) sin(x y) = sin x cos y cos x sin y cos(x y) = cos x cosy sin x sin y

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

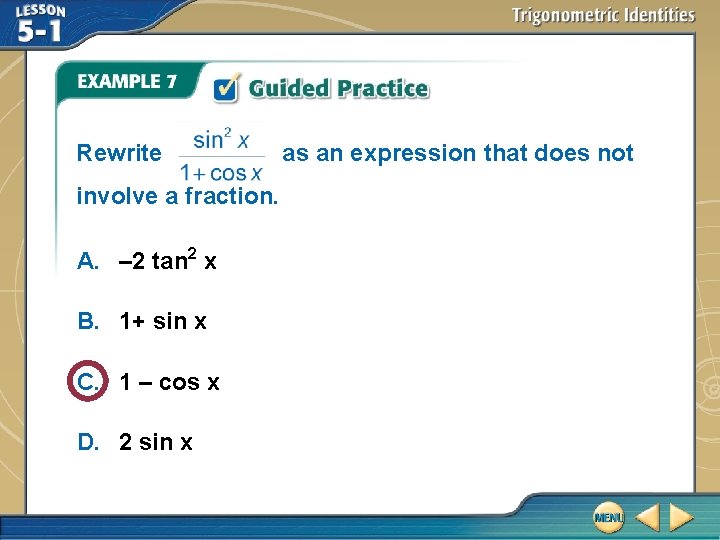
Lesson 5 1 Trigonometric Identities Fiveminute Check Over

Trigonometric Identities Questions Solve the below practice questions based on the trigonometry identities that will help in understanding and applying the formulas in an effective way Express the ratios cos A, tan A and sec A in terms of sin A Prove that sec A (1 – sin A)(sec A tan A) = 1 Find the value of 7 sec 2 A – 7 tan 2 ADefinitions Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse The six trigonometric functions are defined for every real number, except, for some of themFor which sin q = 5 cos q, giving your answers to 1 decimal place (3) June 06 Q6 5 (a) Show that the equation 3 sin2 q – 2 cos2 q = 1 can be written as

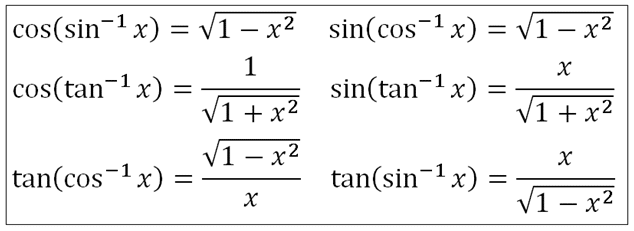
Inverse Trig Identities Reciprocal Of Trigonometric Function Trig

Solved 1 Using Various Trig Identities Determine The Ex Chegg Com

Trigonometric identities are equalities involving trigonometric functions An example of a trigonometric identity is sin ⁡ 2 θ cos ⁡ 2 θ = 1 \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identities501 Fundamental Trigonometric Identities Part A This is an original lesson based on OpenStax Precalculus lesson 71 Summary In this section, you will Use fundamental identities to evaluate trigonometric expressions Use fundamental identities to simplify trigonometric expressionsThe Pythagorean identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan( − θ) = − tanθ cot( − θ) = − cotθ

Revision Trigonometry Siyavula

Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

Trigonometric Formulas like Sin 2x, Cos 2x, Tan 2x are known as double angle formulas because these formulas have double angles in their trigonometric functions Let's discuss Tan2x Formula Tan2x Formula = \\frac{2\text{tan x}}{1 tan^{2}x}\Proving Trig Identities (StepbyStep) 15 Powerful Examples!Trigonometric Identities prove cot (2x)= (1tan^2 (x))/ (2tan (x))

Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube

14 2 Trigonometric Identities

Identities involving trig functions are listed below Pythagorean Identities sin 2 θ cos 2 θ = 1 tan 2 θ 1 = sec 2 θ cot 2 θ 1 = csc 2 θ Reciprocal IdentitiesThe key Pythagorean Trigonometric identity is sin2(t) cos2(t) = 1 tan2(t) 1 = sec2(t) 1 cot2(t) = csc2(t)Let's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1 − c o s ( 2 θ) = 2 s i n 2 ( θ)

5 1 Fundamental Trig Identities Reciprocal Identities Sin

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2The eight basic trigonometric identitiesare listed in Table 1 As we will see, they are all derived from the definition of the trigonometric functions Since many of the trigonometric identities have more than one form, we list the basic identity first and then give the most common equivalent forms 796 111 Introduction to Identities TABLE 1The next set of fundamental identities is the set of reciprocal identities, which, as their name implies, relate trigonometric functions that are reciprocals of each other See Table 3 Recall that we first encountered these identities when defining trigonometric functions from right angles in Right Angle Trigonometry

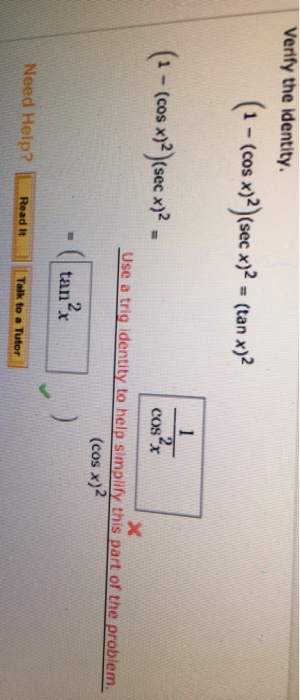
Solved Verify The Identity 1 Cos X 2 Sec X 2 Tan Chegg Com

Trigonometric Identities List Of Trigonometric Identities Examples

Cofunction And Reduction Identities

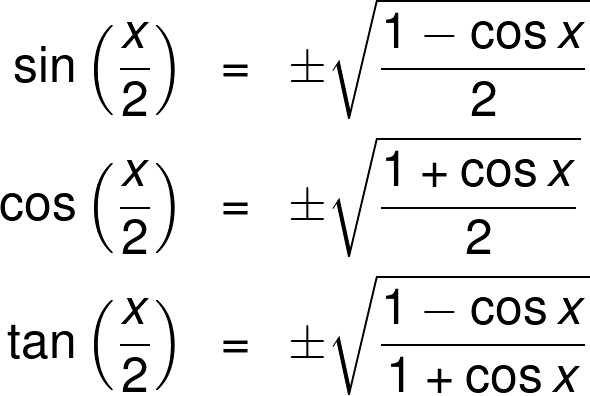
Half Angle Calculator

List Of Trigonometric Identities Wikipedia

Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download

Trigonometric Identities Topics In Trigonometry

3

14 2 Trigonometric Identities

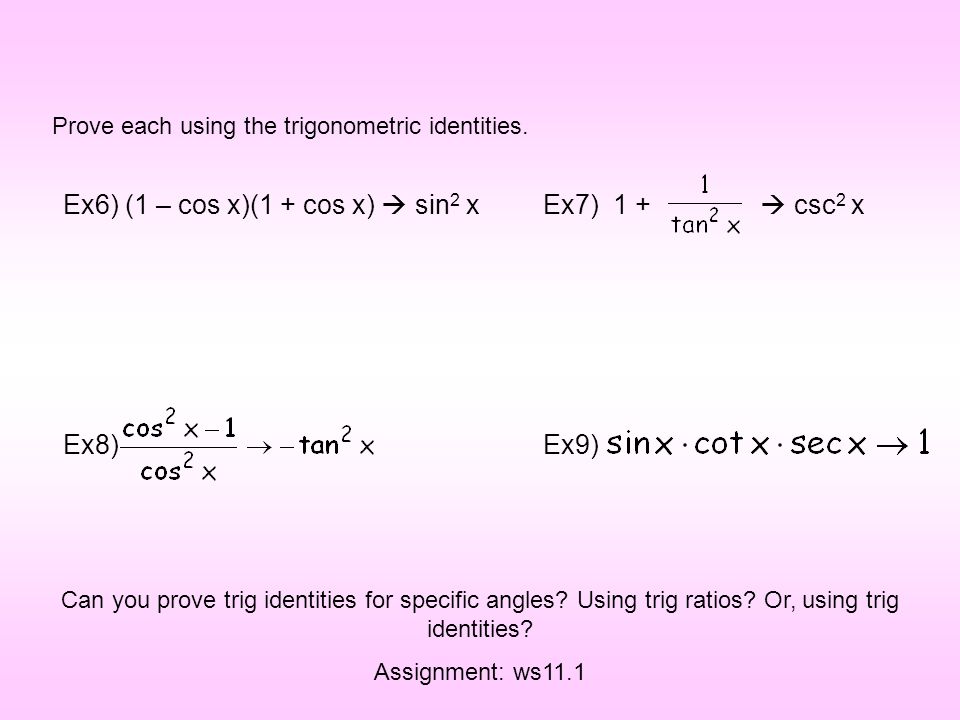
Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Solved 2 Prove The Following Trig Identities A Prove Chegg Com

Http Tutorial Math Lamar Edu Pdf Trig Cheat Sheet Reduced Pdf

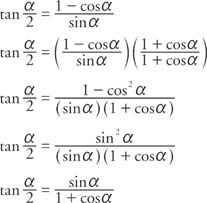
Tangent Identities

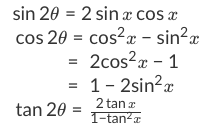
How To Use Double Angle Identities Studypug

1

Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

Http Www Mpsaz Org Rmhs Staff Lxcoleman Trig Test Practice Files 6 Review For Trig Test Pdf

5 1 Trigonometric Identities

Summary Of Trigonometric Identities

How To Prove Quotient And Reciprocal Identities Studypug

3 1 Reciprocal And Pythagorean Identities Mathematics Libretexts

Trig Identities Bingo Card

Worksheet On Trigonometric Identities Establishing Identities Hints

Trig Identities Bingo Card

Www Brockport Edu Academics Tutoring Docs Trigonometric Identities Pdf

Trig Identities All List Of Trigonometric Identities Learn Trigonometry

C330 Trig Functions Tan Gents And Other Things Of Interest

7 Proving Ids Trig Functions Identities

Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero

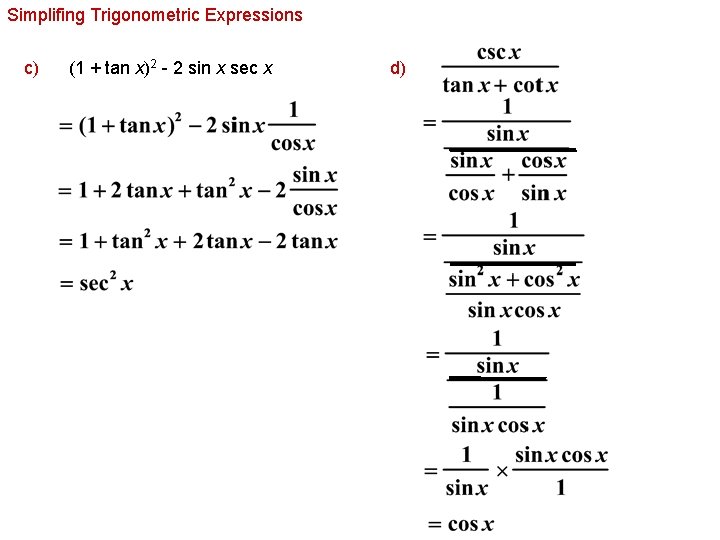
While You Wait Trigonometric Identities And Equations Section

How I Remember Trig Identities Part 2 Beyond Solutions

Summary Of Trigonometric Identities

Tangent Half Angle Formula Wikipedia

Trigonometric Identities Solutions Examples Videos

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

7 4 Proving Trigonometric Identities In This Unit We Ll Be Using Some Formula S That Are Also Found And Used In Unit 7 2 And 7 3 Here We Ll Be Solving Problems To Show That Both Sides Of The Equation Equal Each Other These Formulas Will Help Solve Some Trig

What Are The Quotient Identities For A Trigonometric Functions Socratic

Trigonometric Identities A Plus Topper

Trig Identities Worksheet With Answers 2

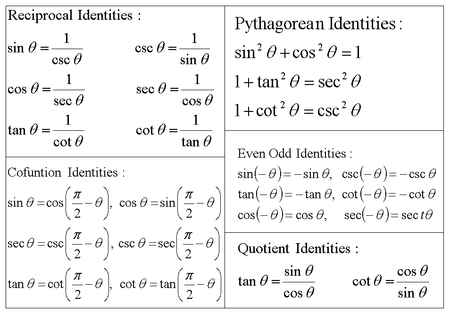
What Does It Mean To Prove A Trigonometric Identity Socratic

14 2 Trigonometric Identities

Summary Of Trigonometric Identities

Verifying Trigonometric Identities How To Do It The Easy Way Lesson Plan Spiral

Trig Identities Maple Learn Maplesoft

Integrate Sec 2x Method 2

Topic 3 Trigonometry Ii

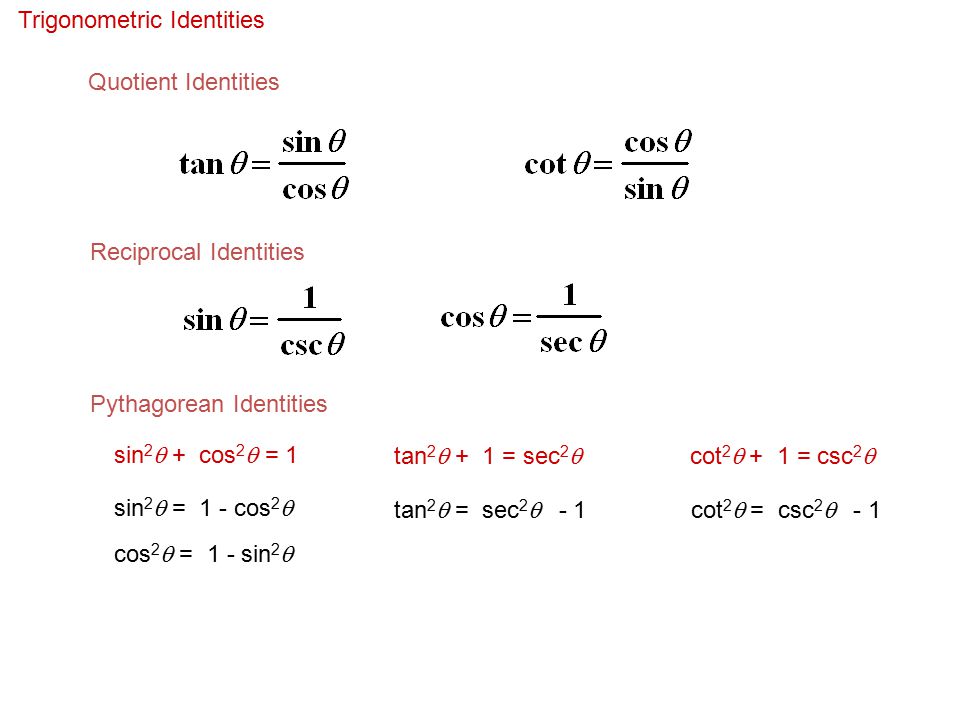
11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download

Derivatives Of Trigonometric Functions

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

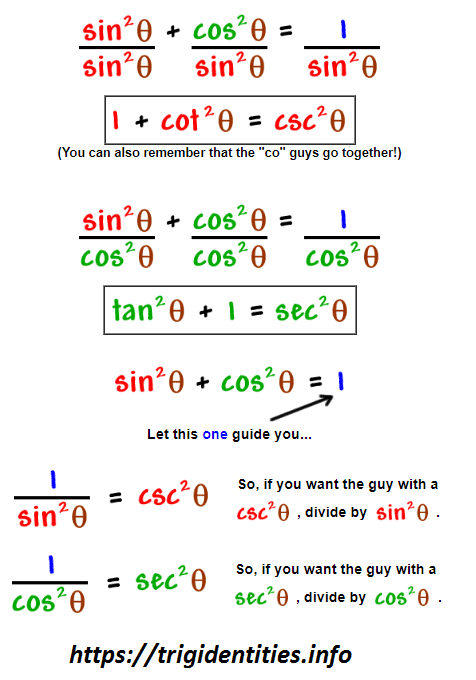
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

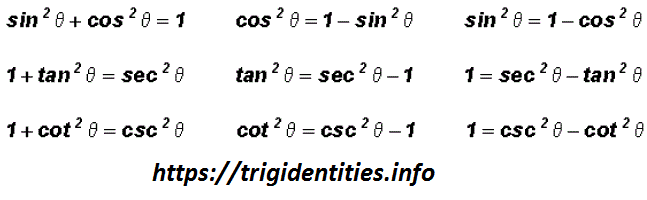
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

3

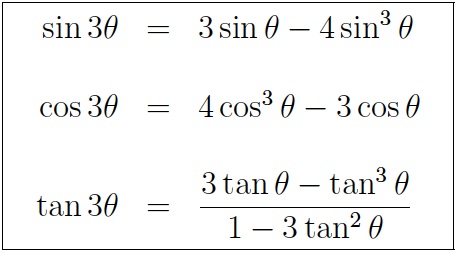
Summary Of Trigonometric Identities

How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube

Tangent Identities

The Trigonometric Ratios Of Angl

Tangent Half Angle Formula Wikipedia

Solved 2 Prove The Following Trig Identities A Prove T Chegg Com

Derivatives Of Trigonometric Functions Web Formulas

Powers Of Trigonometric Functions

14 2 Trigonometric Identities

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

Chapter 11 Trigonometric Identities And Equations 11 1

Precalculus Trigonometry Trig Identities 47 Of 57 Solve Tan 2 Theta 4 0 Theta Youtube

Integrate Sec 2x Method 1

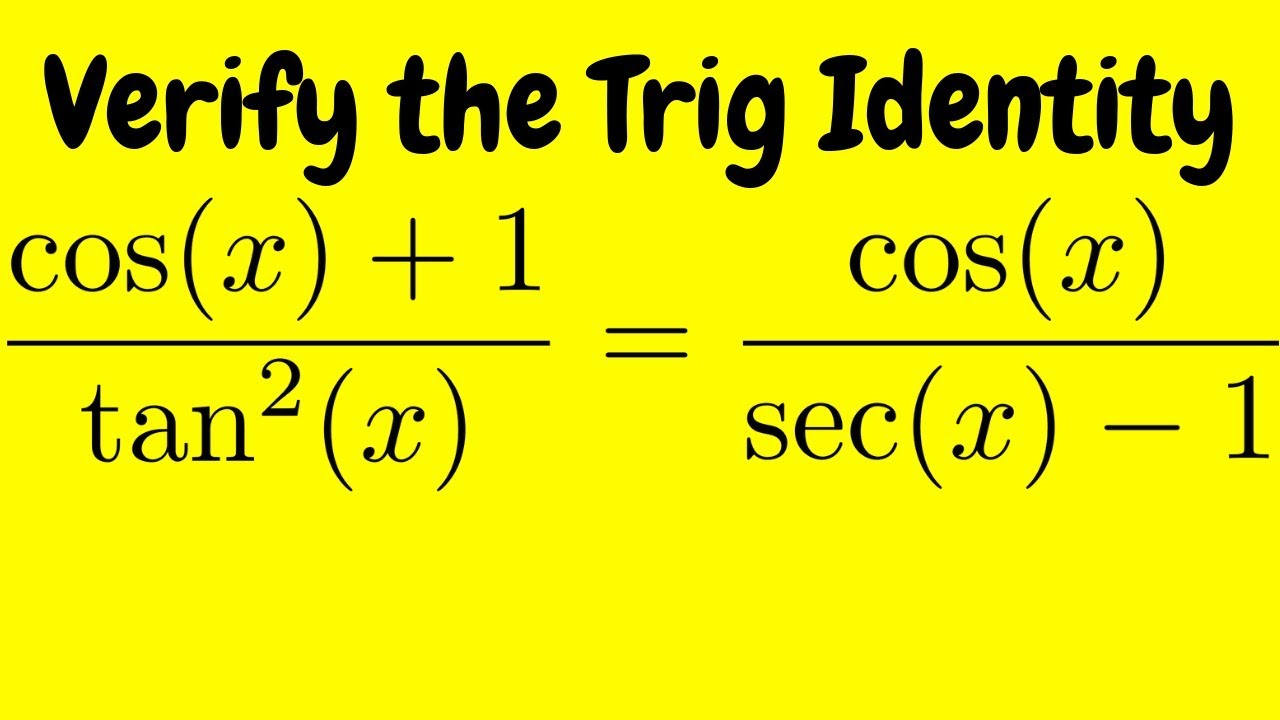
Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube

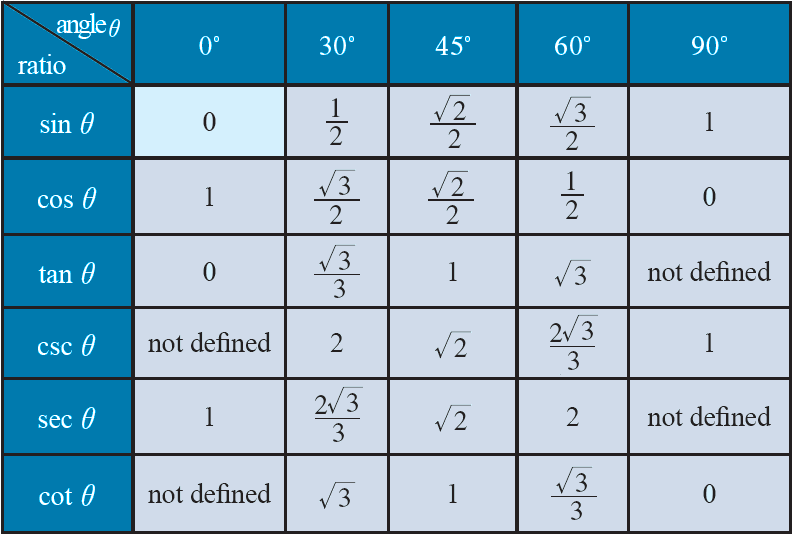
Trigonometric Identities

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

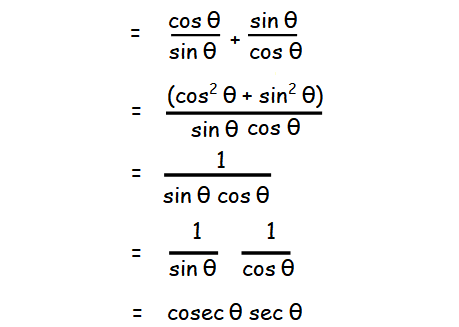
Proving Trigonometric Identities

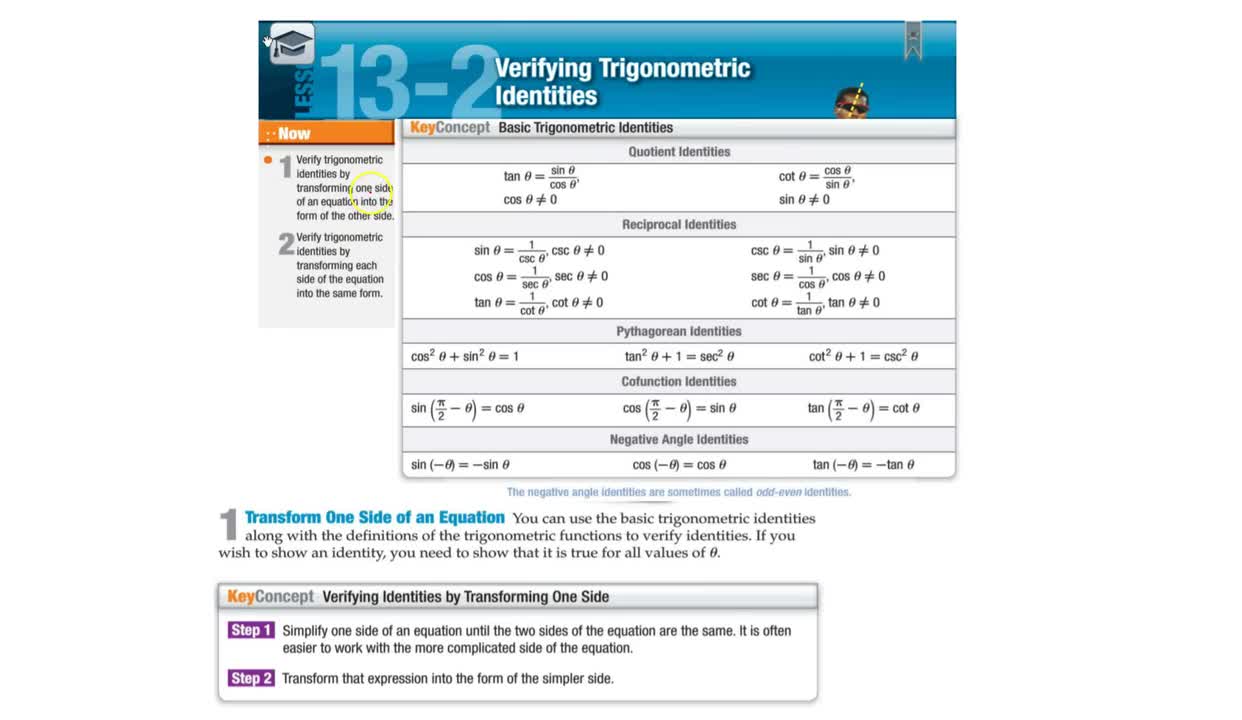
Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School

Ilectureonline

7 4 Proving Trigonometric Identities Mhf4utrigonometry

10 4 Integration Of Powers Of Trigonometric Functions

Trigonometric Identities A Plus Topper

How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic

How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic

Solved We Wish To Prove The Following Trig Identity Tan Chegg Com

What Is The Formula Of Tan2x Quora

Incoming Term: trig identities tan^2,